susinlee 님의 블로그
[250518] TIL 본문
RNN에 대해 공부해보자.
앞서 배웠던 MLP나 CNN은 입력 → 출력이 한 방향으로만 흐르는 구조였다.
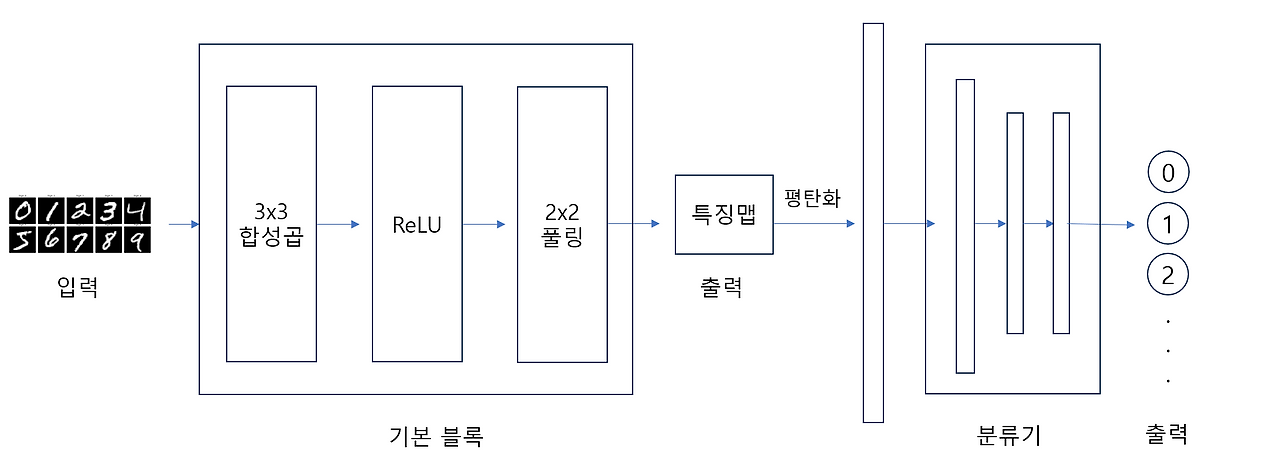
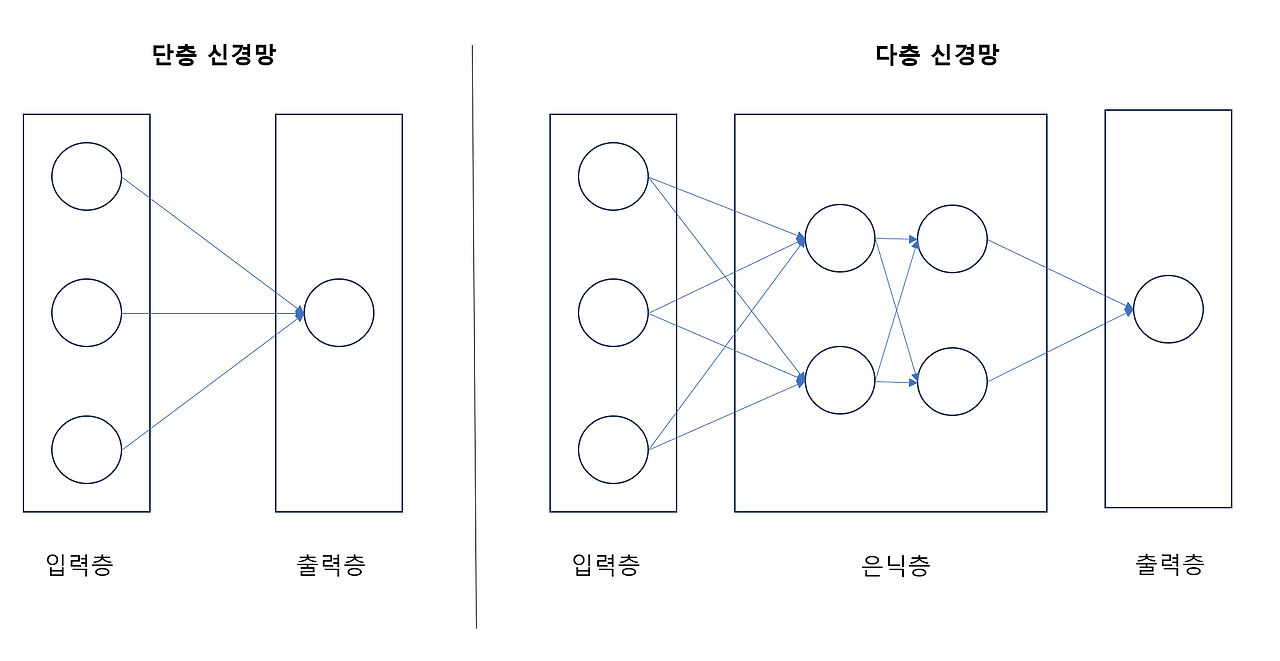
이렇게 입력에서 출력까지 정보가 한 방향으로 흐르는 신경망을 FFNN(Feed-forward Neural Network)라고 한다. 하지만 실제 문제에서는 문장이나 주가, 음성처럼 시간에 따른 순차적인 데이터들이 많다. 이러한 경우에는 과거의 정보가 현재의 판단에 영향을 미치는 구조가 필요하다.
예를 들어, "눈" 이라는 단어는 문맥에 따라 하늘에서 내리는 눈일 수도 있고, 사람의 눈일 수도 있다. 단어 하나만 놓고 보면 어떤 의미인지 알기 어렵지만, 앞에 "첫" 이라는 단어가 붙어 "첫눈"이 된다면 이는 하늘에서 내리는 눈을 의미할 가능성이 높아진다. 이전의 단어(과거 정보)가 현재 단어의 의미 판단에 결정적인 역할을 한다.
이러한 특성을 처리하기 위해 과거 정보를 기억할 수 있는 구조, RNN(Recurrent Neural Network)이 등장하게 된다.
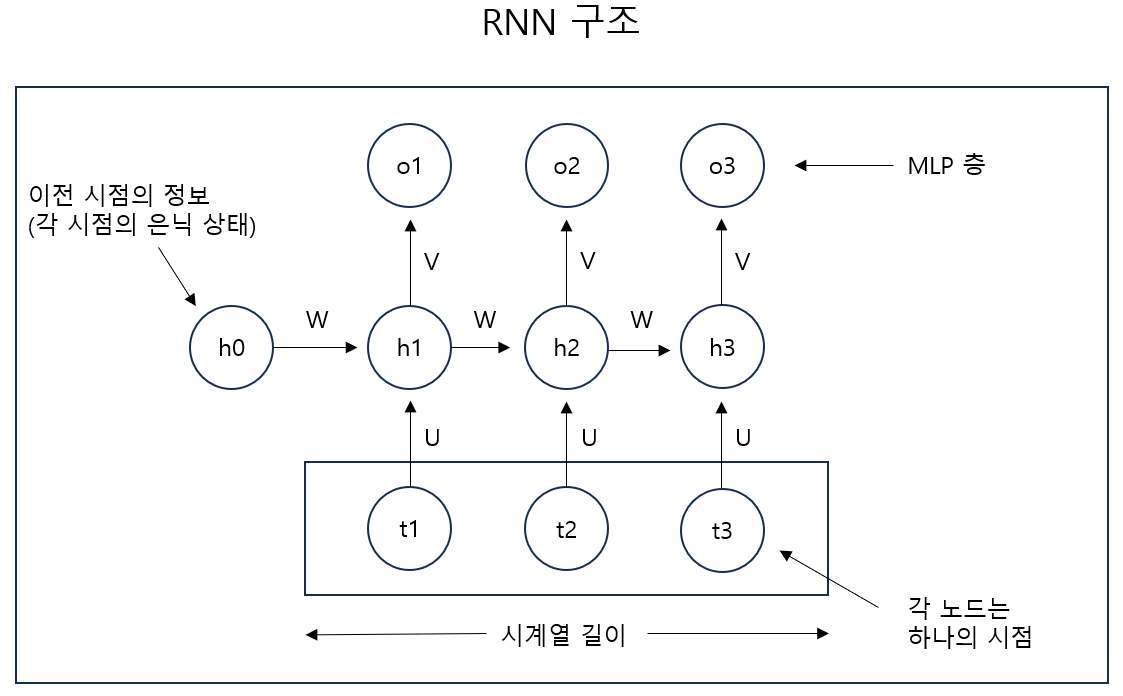
실제로 RNN 모델을 통해 주가를 예측해보자. 입력 특성으로는 시가, 고가, 저가를 사용하고, 예측하고자 하는 것은 다음 날의 종가라고 하자. 이때 우리는 시계열 길이를 어느 정도로 할 것인지 선택해야 한다. 30일로 설정한다면 아래와 같은 형태의 예측 모델을 만드는 것이다.
| 입력 | 정답 |
| 1번째 ~ 30번째 (시가, 고가, 저가) | 31번째 종가 |
| 2번째 ~ 31번째 (시가, 고가, 저가) | 32번째 종가 |
| 3번째 ~ 32 번째 (시가, 고가, 저가) | 33번째 종가 |
| ... | ... |
시계열 데이터가 총 1000개 시점 존재한다고 가정하면 우리는 이 데이터를 순서를 유지한 채로 30개씩 묶어 사용하므로 총 1000 - 30 = 970 개의 데이터 샘플을 생성할 수 있다.
사용한 특성은 시가, 고가, 저가로 3개이므로 각 시점의 입력 차원은 3이 된다. CNN 모델이 채널 수를 늘려 더 많은 표현을 학습하듯이 RNN도 지정한 크기만큼 각 시점의 은닉 상태 차원을 늘려 더 많은 표현을 학습할 수 있다. 또한 RNN 역시 여러 층을 쌓아 깊은 네트워크를 형성할 수 있지만 너무 많이 쌓을 경우 기울기 소실 문제가 발생할 수 있으므로 일반적으로 3 ~ 5층 정도가 적당하다.
class RNN(nn.Module):
# 모델 초기화
def __init__(self):
super(RNN, self).__init__()
# 1. RNN층의 정의
self.rnn = nn.RNN(input_size=3, hidden_size=8, num_layers=5, batch_first=True)
# 2. MLP 층
self.fc1 = nn.Linear(in_features=240, out_features=64)
self.fc2 = nn.Linear(in_features=64, out_features=1)
# 3. 활성화 함수
self.relu = nn.ReLU()
# 순전파 함수 정의
def forward(self, x, h0=None):
if h0 is None:
h0 = torch.zeros(self.rnn.num_layers, x.size(0), self.rnn.hidden_size).to(x.device)
# 1. RNN층의 출력
x, hn = self.rnn(x, h0)
# 2. MLP층의 입력으로 사용되게 모양 변경
x = x.contiguous().view(x.size(0), -1)
# 3. MLP층을 이용해 종가 예측
x = self.fc1(x)
x = self.relu(x)
x = self.fc2(x)
# 4. 예측한 종가를 1차원 벡터로 표현
x = x.squeeze(-1)
return xbatch_first=True 옵션을 설정하면 RNN의 출력 텐서는 [배치 크기, 시퀀스 길이, 은닉 상태 차원] 형태가 된다. 예를 들어, 배치 크기 32, 시퀀스 길이 30, 은닉 상태 차원 8인 경우, 출력 텐서의 크기는 [32, 30, 8] 이 된다. 이 출력값은 하이퍼볼릭 탄젠트 함수를 통과한 후, 최종 예측을 위해 MLP층으로 전달된다. 이때 두 가지 방법이 있다.
1. 전체 시퀀스를 평탄화하여 MLP에 전달
- 출력 텐서 [32, 30, 8] 을 [32, 240] 으로 변형
- 시퀀스의 모든 시점의 정보를 활용하는 방식이다.
2. 마지막 시점의 은닉 상태만 사용
- 출력 텐서에서 마지막 시점만 선택하여 [32, 8] 형태로 전달
- 시퀀스 전체의 정보를 요약한 마지막 상태만 활용한다.
전체 시퀀스를 평탄화하면 모든 시점의 정보를 활용하므로 더 많은 패턴을 학습할 수 있지만, 연산량 증가와 과적합 위험이 따르고, 마지막 시점만 사용할 경우 모델이 더 단순해져서 일반화에 유리하지만, 중간 시점의 정보 손실이 있을 수 있다.
실제 보유중인 주식의 가격 데이터를 불러와서 예측을 수행하였다.
Dataset 클래스로 데이터 세트를 정의했다. pykrx라는 라이브를 통해 보유 주식의 10년치 가격 데이터를 받아왔다. 주식 가격은 기간이 길면 길수록 값의 범위가 넓게 형성되어 있는 편인데, 출력값의 범위가 커지면 오차의 범위가 커지고, 오차가 커지면 역전파되는 기울기 또한 커지게 되기 때문에 가중치 수렴에 안 좋은 영향을 미칠 수 있다. 따라서 각 특성들을 정규화해줄 필요가 있다. 정규화 이후에는 실제 예측을 수행할 때 값의 범위를 원래대로 복원해야하므로 역정규화하는 메소드도 정의해주었다.
# 데이터셋 정의
class mystock(Dataset):
def __init__(self):
self.csv = pd.read_csv('stock_price.csv')
# [시가, 고가, 저가]
self.data = self.csv.iloc[:, 1:4].copy()
self.feature_cols = self.data.columns.tolist()
# 👉 피처별 min-max 정규화
self.data_min = self.data.min()
self.data_max = self.data.max()
self.data = (self.data - self.data_min) / (self.data_max - self.data_min)
# 👉 종가도 따로 정규화 (1차원 벡터)
self.label = self.csv['종가'].copy()
self.label_min = self.label.min()
self.label_max = self.label.max()
self.label = (self.label - self.label_min) / (self.label_max - self.label_min)
self.label = self.label.values # numpy로 변환 (index 제거)
def __len__(self):
return len(self.data) - 30
def __getitem__(self, i):
data_seq = self.data.iloc[i:i+30].values.astype('float32') # [30, 3]
label_val = self.label[i + 30] # 스칼라
data = torch.tensor(data_seq, dtype=torch.float32)
label = torch.tensor(label_val, dtype=torch.float32)
return data, label
def inverse_transform_label(self, norm_label: float) -> float:
"""정규화된 종가 → 원래 가격"""
return norm_label * (self.label_max - self.label_min) + self.label_min
def inverse_transform_data(self, norm_data: torch.Tensor) -> pd.DataFrame:
"""[30, 3] 텐서를 DataFrame으로 역정규화"""
norm_np = norm_data.cpu().numpy() # [30, 3]
denorm = norm_np * (self.data_max.values - self.data_min.values) + self.data_min.values
return pd.DataFrame(denorm, columns=self.feature_cols)
정규화 방식에는 여러가지가 있지만 대표적인 두 방식을 살펴보자.
MinMax 정규화
- 범위를 [0, 1]로 고정시켜 인공 신경망에서 안정적인 학습이 가능하다. RNN, LSTM 등에서 빠른 수렴이 가능하다.
- 이상치에 매우 민감하다. 거래량처럼 스케일이 커지거나 갑자기 급등하는 값이 있으면 전체 분포가 왜곡된다.
Z-Score 정규화
- 평균 0, 표준편차 1로 표준화되기 때문에 이상치에 덜 민감하여 거래량처럼 분포가 비대칭적인 변수에 적합하다.
- 입력값이 음수가 되므로 ReLU나 tanh 등과의 조합에 주의가 필요하다.
데이터에 편향된 분포나 이상치가 존재하는 경우, 먼저 로그 스케일링을 적용한 뒤 MinMax 정규화를 사용하기도 한다. 로그 스케일링은 분포를 보다 완만하게 만들어주며, 특히 0 근처의 작은 값들도 상대적으로 잘 보존할 수 있다는 장점이 있다. 이후 MinMax 정규화를 통해 모델이 안정적으로 학습할 수 있도록 값의 범위를 [0, 1] 로 조정한다.
다음으로 데이터를 훈련 세트(80%)와 테스트 세트(20%)로 나누었다. 시계열 데이터는 순서가 중요한 특성을 가지므로, 일반적인 데이터처럼 무작위로 섞으면 안된다. 따라서 순서를 유지한 채 앞부분은 훈련에, 뒷부분은 테스트에 사용하였다. 가장 최근 시점의 데이터를 테스트 세트로 활용하는 것이 일반적이다. 또한 훈련 세트와 테스트 세트를 나눌 때에는 반드시 훈련 세트를 기준으로 정규화를 수행해야 한다. 전체 데이터를 기반으로 정규화를 진행하면, 테스트 데이터의 통계 정보가 정규화 과정에 포함되어 모델이 미래 정보를 미리 보는 것과 같은 정보 누수가 발생하기 때문이다. 이러면 모델의 성능을 과도하게 높게 평가하는 왜곡된 결과를 초래할 수 있다.
PyTorch의 Subset을 사용하여 데이터 셋을 나눈 후, 이를 DataLoader에 전달하였다. 각 샘플이 시계열 단위로 이미 구성되어 있기 때문에(Dataset에서 정의) 순서를 섞는다고 해서 정보 누수나 순서 왜곡이 일어나지 않는다. 따라서 shuffle=True 옵션을 설정해도 무방하다.
full_df = pd.read_csv('data/stock_price_005710.csv')
features = full_df.iloc[:, 1:4]
labels = full_df['종가']
train_end = int(len(features) * 0.8)
# 👉 훈련 세트 기준으로 min/max 추출
train_features = features.iloc[:train_end]
data_min = train_features.min()
data_max = train_features.max()
train_labels = labels.iloc[:train_end]
label_min = train_labels.min()
label_max = train_labels.max()
# 👉 전체 데이터 정규화 (훈련 기준)
norm_features = (features - data_min) / (data_max - data_min)
norm_labels = (labels - label_min) / (label_max - label_min)
# 👉 Dataset 클래스에 정규화된 데이터와 min/max 전달
dataset = Daewon(norm_features, norm_labels, data_min, data_max, label_min, label_max)
# 시퀀스 기준으로 훈련/테스트 분리
label_n = len(dataset)
train_end = int(label_n * 0.8)
train_set = Subset(dataset, range(0, train_end))
test_set = Subset(dataset, range(train_end, label_n))
train_loader = DataLoader(train_set, batch_size=32, shuffle=True)
test_loader = DataLoader(test_set, batch_size=32)
# 모델 초기화 및 학습
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = RNN().to(device)
optim = Adam(params=model.parameters(), lr=0.0001)
criterion = nn.MSELoss()
model.train()
iterator = tqdm.tqdm(range(100))
for epoch in iterator:
for data, label in train_loader:
optim.zero_grad()
data = data.float().to(device)
label = label.float().to(device)
pred = model(data)
loss = criterion(pred, label)
loss.backward()
optim.step()
# 모델 저장
torch.save(model.state_dict(), 'daewon.pth')
# 장비 및 모델 불러오기
# model.load_state_dict(torch.load('daewon.pth', map_location=device, weights_only=True))
model.eval()
preds, actuals = [], []
total_loss = 0
criterion = nn.MSELoss()
with torch.no_grad():
for data, label in test_loader:
data = data.to(device)
label = label.to(device)
pred = model(data)
# 역정규화
for p, l in zip(pred, label):
pred_val = dataset.inverse_transform_label(p.item())
label_val = dataset.inverse_transform_label(l.item())
preds.append(pred_val)
actuals.append(label_val)
total_loss += criterion(pred, label).item()
avg_loss = total_loss / len(test_loader)
denorm_mse = avg_loss * (label_max - label_min) ** 2
denorm_rmse = (avg_loss ** 0.5) * (label_max - label_min)
# 📈 시각화
x = range(train_end + 30, len(full_df))
plt.figure(figsize=(12, 5))
plt.plot(x, preds, label='예측값')
plt.plot(x, actuals, label='실제값')
plt.title(f'예측 결과 (MSE: {denorm_mse:.2f} 원$^2$, RMSE: {denorm_rmse:.2f} 원)')
plt.xlabel('시간')
plt.ylabel('종가 (원)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
테스트 세트로 예측을 수행한 후 시각화한 그래프이다. 실제값과 예측값 사이에 평균적으로 170원 정도의 차이를 보였다. 최신 데이터를 기반으로 다음 주 월요일 주가도 예측해보자.
# 🔹 마지막 30일치 입력 시퀀스 (정규화된 상태)
# 이미 norm_features로 정규화된 상태에서 Dataset 구성됨
last_input_norm = dataset.data.iloc[-30:].values.astype('float32') # [30, 3]
# 🔹 텐서 변환 + 배치 차원 추가 → RNN 입력 형태: [1, 30, 3]
last_input_tensor = torch.tensor(last_input_norm, dtype=torch.float32).unsqueeze(0).to(device)
# 🔹 예측 (모델은 이미 정규화된 데이터를 학습했음)
model.eval()
with torch.no_grad():
pred_norm = model(last_input_tensor).item()
pred_price = dataset.inverse_transform_label(pred_norm)
# 🔹 출력
print(f"📌 마지막 30일 데이터를 기반으로 한 다음 날 종가 예측: {pred_price:.2f} 원")
(현재 8600원인데 8020원은 좀.... ㅠ)
이렇게 RNN은 주가 예측처럼 시간의 흐름에 따라 변화하는 데이터를 다룰 때 활용할 수 있다. 하지만 주가 예측에서는 다음과 같은 이유로 널리 사용되지 않는다.
1. 주가는 노이즈 심하고 외부 요인에 민감하다.
- 주가는 뉴스나 기업이슈, 지정학적 리스크 등 외부 변수에 의해 급변하기 때문
2. 장기 의존성 문제가 여전히 존재한다.
- RNN은 과거 정보를 은닉 상태로 전달하지만, 시간이 길어질수록 정보가 소멸하거나 왜곡된다.
- 주가는 장기 추세, 계절성, 사이클 등 멀리 떨어진 정보가 중요한 경우도 많다.
3. 학습과 해석이 어렵고 느리다.
- 주가 예측은 투자를 하기 위함이므로 해석력 있는 모델이 선호된다. 하지만 RNN은 왜 이런 결과가 나왔는지 설명하기 어렵다.
몇 가지 테스트를 진행하였고 결과는 다음과 같았다.

성능은 (거래량 미포함 + 모든 시점), (거래량 포함 데이터 + 마지막 시점)이 좋았꼬, 각각 월요일 주가를 8020원, 8160원으로 예측하였다. 월요일에 가격이 얼마일지 한번 비교해봐야겠다.
모델의 역사와 흐름을 알아둘 필요가 있다. 앞으로 내가 가야할 길이기 때문에... 선배님들이 열심히 다져놓은 길을 열심히 따라가보자.
1. 머신러닝/딥러닝 모델의 역사
| 시기 | 모델 |
| 1950 ~ | 선형 회귀, 퍼셉트론 |
| 1980 ~ | MLP(다층 퍼셉트론), 오차 역전파 알고리즘 |
| 1990 ~ | SVM, k-NN, 앙상블(Bagging, Boosting) |
| 2000 ~ | CNN, RNN |
| 2010 ~ | LSTM, GRU, GAN, AutoEncoder |
| 2017 ~ | Transformer, BERT, GPT, Diffusion |
2. 시계열 / 자연어 모델의 흐름 (Squence Modeling)
| 연도 | 모델 | 특징 |
| 1980 ~ | RNN | 최초의 순환 신경망. 시계열/텍스트 데이터를 시간 순서대로 처리 가능 |
| 1997 | LSTM | RNN의 기울기 소실 문제 해결. 장기 기억 가능 |
| 2014 | GRU, Seq2Seq | LSTM의 간소화 버전(GRU), Seq2Seq 번역, 요약 등에 사용됨 |
| 2015 | Attention | 중요한 입력 위치에 가중치를 주는 메커니즘 등장 |
| 2017 | Transformer | Attention만으로 구성된 모델. 순차 처리 없이 전체 문맥 참조 가능 |
| 2018 | GPT-1 | Transformer 기반의 생성형 언어 모델. Pretrain-Finetune 구조 |
| 2019 ~ | BERT, GPT-2, 3, 4 | 다양한 파생 모델 등장. 자연어 분야 주도 |
3. 이미지 처리 모델의 흐름 (Computer Vision)
| 연도 | 모델 | 특징 |
| 1998 | LaNet-5 | 손글씨 숫자 인식. 최초의 CNN 구조 |
| 2012 | AlexNet | ImageNet 대회 우승. 딥러닝 붐의 시발점 |
| 2014 | VGGNet | 단순한 3x3 conv만 쌓은 구조로 이해와 구현 용이 |
| 2015 | ResNet | Skip Connection으로 딥러닝에서 gradient 소실 해결 |
| 2016 | Inception | 다양한 필터를 병렬로 사용. 구조 최적화 |
| 2020 | ViT (Vision Trnasformer) | CNN 없이 Transformer로 이미지를 처리 |
4. 시계열 예측 특화 모델의 흐름
| 연도 | 모델 | 특징 |
| 1980 ~ | ARIMA | 통계 기반 시계열 예측 모델 |
| 2000 ~ | RNN | 순환 신경망으로 시계열 데이터 처리 |
| 2014 | LSTM/GRU | 장기 의존성 문제 해결. 주가/IoT 예측 등에 사용 |
| 2017 | Seq2Seq + Attention | 멀티스텝 예측 강화. 입력 시퀀스 → 출력 시퀀스 |
| 2020 | Informer, Transformer-TS | Transformer 구조를 시꼐열에 맞게 수정 |
| 2021 | PatchTST, TimesNet | 시계열에 최적화된 Transformer. 높은 예측 정확도 |
5. 생성 모델의 역사 (이미지/텍스트 생성)
| 연도 | 모델 | 특징 |
| 2014 | AutoEncoder | 입력을 압축하고 복원하는 구조 |
| 2014 | GAN | 진짜 같은 이미지 생성 |
| 2017 | VAE | 확률적 생성 모델 |
| 2018 | GPT | Transformer 기반 텍스트 생성 모델 |
| 2020 ~ | Diffusion | 노이즈를 점차 제거하며 생성. 고해상도 이미지 생성에 강함 (예: DALL-E 2) |
'TIL > TIL' 카테고리의 다른 글
| [250520] TIL (2) | 2025.05.21 |
|---|---|
| [250519] TIL (1) | 2025.05.20 |
| [250515] TIL (0) | 2025.05.16 |
| [250514] TIL (0) | 2025.05.15 |
| [250513] TIL (0) | 2025.05.14 |





